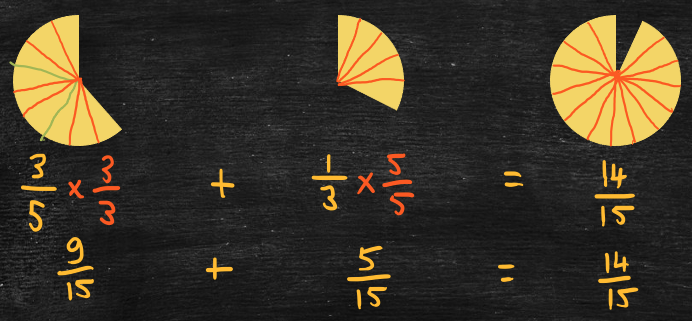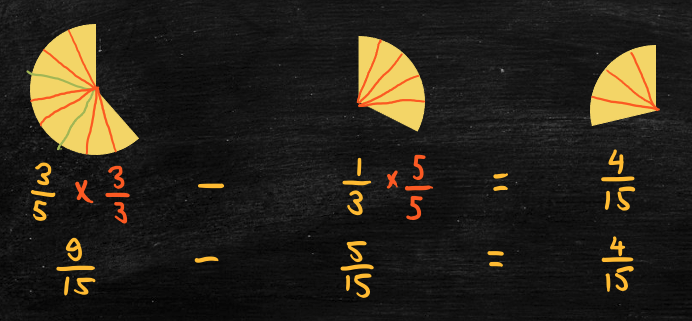2.5: Adding and subtracting fractions

In the following, “A/B” represents the fraction “A over B.” For example, “2/3” refers to the fraction “2 over 3” or “two-thirds.”

Adding fractions

To add two fractions together, the fractions must be expressed using a common denominator (i.e., the parts must be the same size). For example,

• 3/5 + 1/3 (three-fifths plus one-third).
• First, find a common denominator for 5 and 3.
  • Multiples of 5 are 5, 10, 15, …
  • Multiples of 3 are 3, 6, 9, 12, 15, …
  • 15 is the least common multiple, so use 15 as the common denominator.
• Next, express 3/5 and 1/3 using equivalent fractions with denominator 15.
  • In each case, multiply the original fraction by a fraction equal to 1 (either 3/3 or 5/5).
  • Multiply 3/5 by 3/3 to get (3×3)/(5×3) = 9/15.
  • Multiply 1/3 by 5/5 to get (1×5)/(3×5) = 5/15.
• Next, add the numerators of the new fractions (and simplify the resulting fraction if necessary).
  • 9/15 + 5/15 = 14/15.
  • This works because 9/15 represents 9 parts each of size 1/15 and 5/15 represents 5 parts each of size 1/15.
  • Since all the parts are the same size we can add them together.

Subtracting fractions

To subtract one fraction from another fraction, again the fractions must be expressed using a common denominator. For example,

• 3/5 – 1/3 (three-fifths minus one-third).
• First, find a common denominator for 5 and 3.
  • 15 is the least common multiple, so use 15 as the common denominator.
• Next, express 3/5 and 1/3 using equivalent fractions with denominator 15.
  • Multiply 3/5 by 3/3 to get (3×3)/(5×3) = 9/15.
  • Multiply 1/3 by 5/5 to get (1×5)/(3×5) = 5/15.
• Next, subtract the numerators of the new fractions (and simplify the resulting fraction if necessary).
  • 9/15 – 5/15 = 4/15.

The video below works through some examples of adding and subtracting with fractions.