3.3: Multiplying fractions

In the following, “A/B” represents the fraction “A over B.” For example, “2/3” refers to the fraction “2 over 3” or “two-thirds.” In the fraction, A/B, “A” is called the numerator and “B” is called the denominator.

To multiply two fractions together, multiply the numerators and the denominators separately, then simplify if necessary. For example,

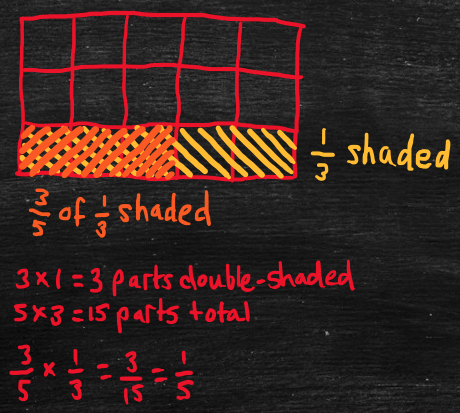
• 3/5 x 1/3 (three-fifths times one-third).
• First, multiply the numerators: 3 x 1 = 3.
• Next, multiply the denominators: 5 x 3 = 15.
• Finally, simplify: 3/15 is equivalent to 1/5 (see 1.3: Simplifying fractions).
• This works because “3/5 x 1/3” represents “three-fifths of one-third.”
  • Divide a unit rectangle into thirds (horizontally) and shade one-third.
  • Divide the rectangle into fifths (vertically) and double-shade three-fifths of the shaded one-third.
  • The number of double-shaded parts is 3 x 1 = 3 (the product of the numerators).
  • The total number of parts is 5 x 3 = 15 (the product of the denominators).
  • The answer is the number of double-shaded parts (3) divided by the total number of parts (15), i.e., 3/15, which simplifies to 1/5.

The video below works through some examples of multiplying fractions.