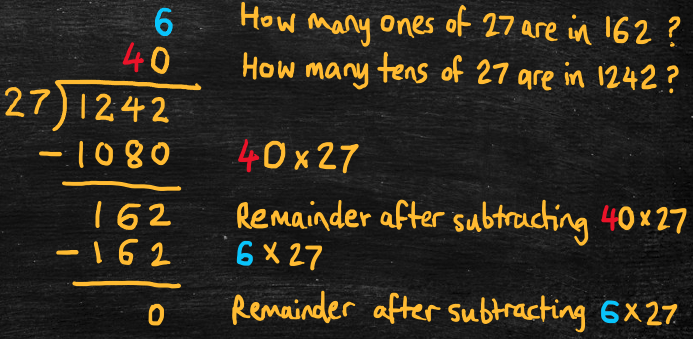4.1: Dividing integers

Scaffold method

To divide two integers (e.g., A ÷ B), repeatedly subtract product of 10 multiples of the divisor (B) from the dividend (A). The result of the division is called the quotient. For example,

• 1242 ÷ 27 = ?
• 100 x 27 = 2700, which is greater than 1242, so start with the tens place value
• 40 x 27 = 1080, so the tens digit of the quotient is 4    [50 x 27 = 1350, which is too high]
• 1242 – 1080 = 162    [this is the remainder after subtracting 40 x 27]
• 6 x 27 = 162, so the ones digit of the quotient is 6    [7 x 27 = 189, which is too high]
• 162 – 162 = 0    [i.e., there is no remainder after subtracting 6 x 27]
• The quotient is 40 + 6 = 46 (with no remainder)

Common method

The common method, which is generally called long division, uses the same idea as the scaffold method, but writes the calculations more compactly. For example,

• 1242 ÷ 27 = ?
• 100 x 27 = 2700, which is greater than 1242, so start with the tens place value
• 4 x 27 = 108, so the tens digit of the quotient is 4
• 124 – 108 = 16    [this is the remainder after subtracting 4 x 27]
• Carry down “2”    [this is the ones digit in 1242]
• 6 x 27 = 162, so the ones digit of the quotient is 6
• 162 – 162 = 0    [i.e., there is no remainder after subtracting 6 x 27]
• The quotient is 40 + 6 = 46 (with no remainder)

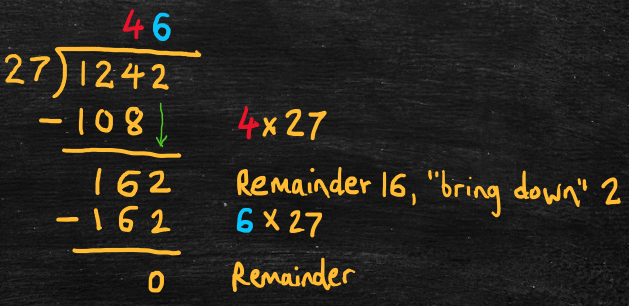
These methods work for dividing a decimal number by an integer too. For example, 124.2 ÷ 27 = 4.6, with the only changes to the calculations above being the insertion of the decimal point in the dividend (124.2) and the quotient (4.6).

The video below works through some examples of dividing integers.