Notes
A function is simply a rule that assigns a unique output value to an input value. For example, the function “multiply the input value by 3 and add 1” would assign an output value of 7 to an input value of 2 (since 3 times 2 plus 1 equals 7).
Equations
We generally write input values using the variable “x” and output values using the variable “y.” Then the equation representing the previous function is y = 3x + 1.
Tables
One way to summarize a function is in a table of input and output values. A table for the function, y = 3x + 1, is as follows:
| Input, x | 0 | 1 | 2 | 3 | 4 |
| Output, y | 1 | 4 | 7 | 10 | 13 |
Graph
Another way to summarize a function is in a graph with the input values (x) plotted on the horizontal axis and the output values (y) plotted on the vertical axis. A graph for the function, y = 3x + 1, is as follows:
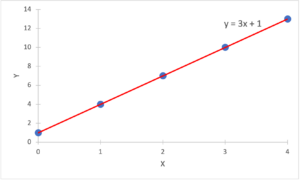
The plotted points on the graph are written in pairs with x first and y second, e.g., (x, y) = (1, 4).
Linear functions
There are many different types of function, but the most important function in elementary math is the linear function. Linear functions have the form y = mx + c, where m is the slope and c is the y-intercept.
- The slope, m, is the change in y ÷ the change in x
- The y-intercept, c, is the value of y when x is 0
In a graph for a linear function, if the slope is positive, the graph slopes up to the right. If the slope is negative, the graph slopes down to the right. The y-intercept is where the graph crosses the vertical axis.
For the function, y = 3x + 1, the slope, m, is 3 because y changes by 3 when x changes by 1. For example, when x changes from 0 to 1 (an increase of 1), y changes from 1 to 4 (an increase of 3). Similarly, when x changes from 1 to 2 (an increase of 1), y changes from 4 to 7 (an increase of 3).
For the function, y = 3x + 1, the y-intercept, c, is 1 because y is 1 when x is 0.
By the way, if the output numbers for this function look familiar, that’s because they came up in Practice Exercise #3 in 8.1: Sequences. Linear functions are related to arithmetic sequences: the step in an arithmetic sequence is equivalent to the slope in a linear function, while the 0th entry in an arithmetic sequence is equivalent to the y-intercept in a linear function.
Calculating the slope and intercept of a linear function
Consider the linear function represented by the following table and graph:
| Input, x | 0 | 1 | 2 | 3 | 4 |
| Output, y | –1 | 1 | 3 | 5 | 7 |
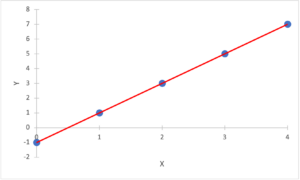
- To calculate the slope, m, find the input and output values of two points and calculate the change in y ÷ the change in x, e.g., (7 – 5) / (4 – 3) = 2 ÷ 1 = 2.
- To calculate the y-intercept, c, find the output value when the input value is 0, e.g., y = –1 when x = 0.
The equation of this linear function is therefore y = 2x – 1.
The table and graph of a linear function may not show the y-intercept explicitly, in which case the y-intercept might need to be calculated by using the slope and a point. For example, suppose we know the slope is 2 and a point on the graph is (x, y) = (2, 3). Then, changing x by –2 (i.e., from 2 to 0) must change y by the slope times the change in x = 2 times –2 = –4 (i.e., y changes from 3 to 3 – 4 = –1).
The video below works through an example of a linear function.
Video Tips
Practice Exercises
Do the following exercises to practice working with linear functions.

