Many area and perimeter calculations in elementary math can be accomplished knowing just a few formulas based on circles, triangles, and rectangles.

• The area of a circle is given by π x r², where r is the radius and π (pi) is the number 3.141592654… For hand calculation, we’ll simply use π = 3.14.
• The circumference of a circle is given by 2 x π x r.
• The area of a triangle is given by (1/2) x b x h, where b is the base and h is the height (perpendicular to the base). Any convenient side of the triangle can be selected as the base.
• We can use the Pythagorean theorem from 9.1: Angles to calculate one side length of a triangle from the other two side lengths.
• The area of a rectangle is given by l x w, where l is the length and w is the width.

Examples

1. Calculate the area of a circle with a radius of 5 cm. Area = π x r² = π x 5² = π x 25 = 25π = 25(3.14) = 78.5 cm².
2. Calculate the circumference of a circle with a radius of 5 cm. Circumference = 2 x π x r = 2 x π x 5 = 10π = 10(3.14) = 31.4 cm.
3. Calculate the area of the following triangle:
   
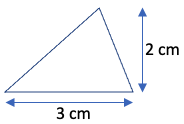
   Area = (1/2) x b x h = (1/2) x 3 x 2 = 3 cm².
4. Calculate the area of the following rectangle:
   
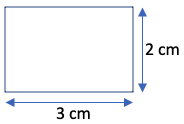
   Area = l x w = 3 x 2 = 6 cm².
5. Calculate the area of the following shape comprised of a half-circle, right triangle, and rectangle:
   
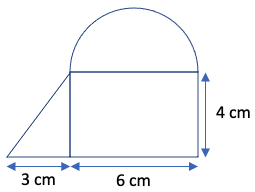
   Half-circle area = (1/2) x π x r² = (1/2) x π x (6/2)² = 4.5π = 4.5(3.14) = 14.13 cm².
   Triangle area = (1/2) x b x h = (1/2) x 3 x 4 = 6 cm².
   Rectangle area = l x w = 6 x 4 = 24 cm².
   Total area = 14.13 cm² + 6 cm² + 24 cm² = 44.13 cm².
6. Calculate the perimeter of the shape in Example 5:
   Half-circle circumference = (1/2) x 2 x π x r = π x (6/2) = 3π = 3(3.14) = 9.42 cm.
   Hypotenuse of right triangle = √(3² + 4²) = √25 = 5 cm.
   Perimeter = 9.42 cm + 5 cm + 3 cm + 6 cm + 4 cm = 27.42 cm.

The video below works through some area and perimeter calculations based on circles, triangles, and rectangles.