6.2: Factors and multiples

Factors and multiples

• A factor of a counting number A is a counting number that divides A evenly with no remainder (i.e., A is divisible by its factors).
• Suppose A, B, and C are counting numbers related by the equation A = B x C.
  • B is a factor of A because A is divisible by B (i.e., A ÷ B = C).
  • C is a factor of A because A is divisible by C (i.e., A ÷ C = B).
• Example: 6 = 2 x 3.
  • 2 is a factor of 6 because 6 is divisible by 2 (i.e., 6 ÷ 2 = 3).
  • 3 is a factor of 6 because 6 is divisible by 3 (i.e., 6 ÷ 3 = 2).
• A multiple of a counting number D is any product of D and another counting number.
• Suppose D, E, and F are counting numbers related by the equation D x E = F.
  • F is a multiple of D because F = D x E.
  • F is a multiple of E because F = E x D.
• Example: 2 x 3 = 6.
  • 6 is a multiple of 2 because 6 = 2 x 3.
  • 6 is a multiple of 3 because 6 = 3 x 2.

Find the factors of a number

• Example: Find the factors of 126.
• Method: Repeatedly divide by counting numbers from 1, record those that divide evenly (with no remainder) together with the resulting quotient (which is also a factor), stop when a quotient would be less than the greatest factor recorded so far.
• Divide by 1: factors are 1 and 126 (since 1 x 126 = 126).
• Divide by 2: factors are 2 and 63 (since 2 x 63 = 126).
• Divide by 3: factors are 3 and 42 (since 3 x 42 = 126).
• Skip 4 and 5 because they don’t divide 126 evenly.
• Divide by 6: factors are 6 and 21 (since 6 x 21 = 126).
• Divide by 7: factors are 7 and 18 (since 7 x 18 = 126).
• Skip 8 because it doesn’t divide 126 evenly.
• Divide by 9: factors are 9 and 14 (since 9 x 14 = 126).
• Skip 10, 11, 12, and 13 because they don’t divide 126 evenly.
• 14 is already in the list of factors (paired with 9).
• Stop because any number larger than 14 will have a quotient less than 9.
• The factors of 126 are 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, and 126.

• Example: Find the factors of 60.
• Divide by 1: factors are 1 and 60 (since 1 x 60 = 60).
• Divide by 2: factors are 2 and 30 (since 2 x 30 = 60).
• Divide by 3: factors are 3 and 20 (since 3 x 20 = 60).
• Divide by 4: factors are 4 and 15 (since 4 x 15 = 60).
• Divide by 5: factors are 5 and 12 (since 5 x 12 = 60).
• Divide by 6: factors are 6 and 10 (since 6 x 10 = 60).
• The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.

Find the multiples of a number

• Example: Find the multiples of 126.
• Method: Repeatedly multiply by counting numbers from 1, record each product. There is no stopping rule because every counting number has an infinite number of multiples!
• Multiply by 1: 1 x 126 = 126, so 126 is a multiple.
• Multiply by 2: 2 x 126 = 252, so 252 is a multiple.
• Multiply by 3: 3 x 126 = 378, so 378 is a multiple.
• The multiple of 126 are 126, 252, 378, …

• Example: Find the multiples of 60.
• Multiply by 1: 1 x 60 = 60, so 60 is a multiple.
• Multiply by 2: 2 x 60 = 120, so 120 is a multiple.
• Multiply by 3: 3 x 60 = 180, so 180 is a multiple.
• The multiple of 60 are 60, 120, 180, …

Common factors of two numbers and the GCF

• We can find common factors of two numbers.
• The largest of these is called the Greatest Common Factor (GCF).
• Note that the term “least common factor” is meaningless since it would always be 1.

Common multiples of two numbers and the LCM

• We can find common multiples of two numbers.
• The smallest of these is called the Least Common Multiple (LCM).
• Note that the term “greatest common multiple” is meaningless since we can continue to find greater common multiples.

Example: find the GCF and LCM of 126 and 60

• Slide Method:
  • Find a common factor of both numbers, write the factor to the left and the resulting quotients below.
  • Repeat until there are no more common factors.
  • The GCF is the product of all the factors written to the left.
  • The LCM is the product of the GCF and the numbers written at the bottom.
• 2 is a common factor of 126 and 60:
  • write 2 to the left,
  • write 126 ÷ 2 = 63 and 60 ÷ 2 = 30 below.
• 3 is a common factor of 63 and 30:
  • write 3 to the left,
  • write 63 ÷ 3 = 21 and 30 ÷ 3 = 10 below.
• 21 and 10 have no common factors:
  • the GCF of 126 and 60 is 2 x 3 = 6,
  • the LCM of 126 and 60 is 6 x 21 x 10 = 1260.
• The following figure illustrates these steps.

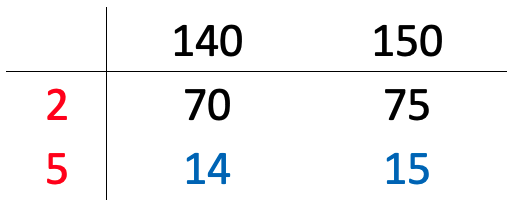
Example: find the GCF and LCM of 140 and 150

• 2 is a common factor of 140 and 150:
  • write 2 to the left,
  • write 140 ÷ 2 = 70 and 150 ÷ 2 = 75 below.
• 5 is a common factor of 70 and 75:
  • write 5 to the left,
  • write 70 ÷ 5 = 14 and 75 ÷ 5 = 15 below.
• 14 and 15 have no common factors:
  • the GCF of 140 and 150 is 2 x 5 = 10,
  • the LCM of 140 and 150 is 10 x 14 x 15 = 2100.

The video below works through some examples of working with factors and multiples .