Notes
Word problems for the division problem, A ÷ B, can either use the “how-many-groups” interpretation of division or the “how-many-units-in-one-group” interpretation.
How many groups?
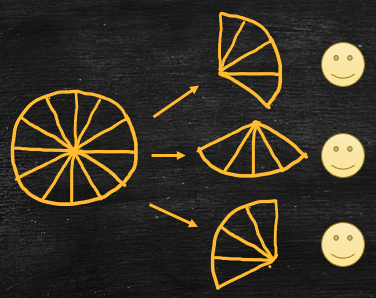
A ÷ B represents, “How many groups are there if A units are divided into groups of B units?” For example,
- Arithmetic problem: Solve 12 ÷ 4.
- Word problem: A pizza cut into 12 slices is to be divided among friends such that each friend gets 4 slices. How many friends can share the pizza?
- 12 ÷ 4 = 3, so 3 friends can share the pizza.
- Here, each friend is a “group,” the pizza slices are the units, and we’re finding the number of friends: 12 slices ÷ 4 slices per fried = 3 friends.
- Equivalently, 3 friends times 4 slices per friend equals 12 slices in total.
How many units in one group?
A ÷ B represents, “How many units are in one group if A units are divided into B groups?” For example,
- Arithmetic problem: Solve 12 ÷ 4.
- Word problem: A pizza cut into 12 slices is to be divided among 4 friends. How many slices do they each get?
- 12 ÷ 4 = 3, so each friend gets 3 slices.
- Again, each friend is a “group” and the pizza slices are the units, but now we’re finding the number of slices per friend: 12 slices ÷ 4 friends = 3 slices per friend.
- Equivalently, 3 slices per friend times 4 friends equals 12 slices in total.

The video below works through some examples of word problems for dividing integers.
Video Tips
Practice Exercises
Do the following exercises to practice matching integer division problems and word problems.

