Notes
Angles measure the rotation in degrees (denoted by a small circle: º) about a fixed point. For example, if you’re facing north and turn 90º to the right, you’ll be facing east. Another 90º turn to the right (or 180º total) and you’ll be facing south. Then, another 90º turn to the right (or 270º total) and you’ll be facing west. Then, another 90º turn to the right (or 360º total) and you’ll be back facing north again.
Lines
An angle can also measure between two lines that meet at a point (called the vertex). The angle measures how much one line would have to rotate about the vertex to line up with the other line.
Four angles are formed when two lines cross. Each pair of opposite angles is equal:
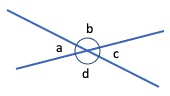
Angles a and c are opposite angles, as are angles b and d:
- angle a = angle c
- angle b = angle d
Also, angles a and b add to 180º and are called supplementary angles. Other supplementary angles here are angles b and c, angles c and d, and angles d and a.
Eight angles are formed when one line crosses two parallel lines. Each pair of corresponding angles is equal.
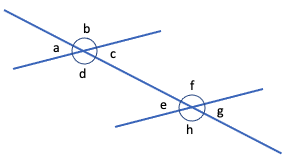
Angles a and e are corresponding angles, as are angles b and f, angles c and g, and angles d and h. The two shorter lines are parallel, so:
- angle a = angle c = angle e = angle g
- angle b = angle d = angle f = angle h
Polygons
Polygons are closed shapes made from (straight, non-crossing) line segments. For example, a polygon made from three line segments is a triangle, a polygon made from four line segments is a quadrilateral, a polygon made from five line segments is a pentagon, and so on. The interior angles in a polygon add up to (n – 2) x 180º, where n is the number of sides. So, the interior angles of a triangle sum to 180º, the interior angles of a quadrilateral sum to 360,º the interior angles of a pentagon sum to 540,º and so on.
If the interior angles of a polygon are all equal (and the side lengths are also all equal), then the polygon is called regular. A regular triangle has 60º interior angles and is called an equilateral triangle. A regular quadrilateral has 90º interior angles and is called a square.
Other types of triangle are:
- an isosceles triangle has (at least) two sides that are the same length
- a scalene triangle has all different side lengths
Other types of quadrilateral are:
- a rectangle has equal (90º) angles
- a rhombus (or diamond) has equal side lengths
- a parallelogram has opposite sides that are parallel
Right angles
An angle of 90º is called a right angle and a triangle with a right angle is called a right triangle. The opposite side of the right angle in a right triangle is called the hypotenuse. The side lengths of a right triangle are related according to the Pythagorean theorem: the square of the hypotenuse is equal to the sum of squares of the other sides. For example:
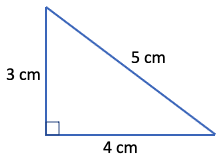
Pythagorean theorem: 52 = 32 + 42 (correct since 25 = 9 + 16).
The Pythagorean theorem can be used to calculate the length of one unknown side of a right triangle. For example:
- If the hypotenuse above was unknown, x = √(32 + 42) = √25 = 5 cm.
- If the left side length was unknown, x = √(52 – 42) = √9 = 3 cm.
- If the bottom side length was unknown, x = √(52 – 32) = √16 = 4 cm.
The video below works through some examples of calculating angles and applying the Pythagorean theorem.
Video Tips
Practice Exercises
Do the following exercises to practice calculating angles and applying the Pythagorean theorem.
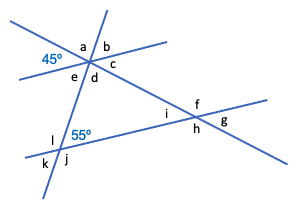
1. Consider the following diagram in which the two lines sloping upwards to the right are parallel.