4.5: Word problems for dividing fractions

In the following, “A/B” represents the fraction “A over B.” For example, “2/3” refers to the fraction “2 over 3” or “two-thirds.” Word problems for the division problem, A/B ÷ C/D, can either use the “how-many-groups” interpretation of division or the “how-many-units-in-one-group interpretation.

How many groups?

A/B ÷ C/D represents, “How many groups are there if A/B units are divided into groups of C/D units?” Another way to say this is, “How many times does C/D go into A/B?” For example,

• Arithmetic problem: Solve 3/8 ÷ 3/4.
• Word problem: A recipe calls for 3/4 of a cup of sugar, but Marybeth only has 3/8 of a cup of sugar. How much of the recipe can Marybeth make?
• Solve by expressing fractions using common denominators and dividing the numerators.
• 3/8 ÷ 3/4 = 3/8 ÷ 6/8 = 3 ÷ 6 = 1/2, so Marybeth can make 1/2 the recipe.
• Here, a recipe is a “group,” cups of sugar are the units, and we’re finding the fraction of a recipe we can make with 3/8 of a cup of sugar. In other words, 3/8 of a cup of sugar ÷ 3/4 of a cup of sugar per recipe = 1/2 a recipe.
• Equivalently, 1/2 a recipe times 3/4 of a cup of sugar per recipe equals 3/8 of a cup of sugar.

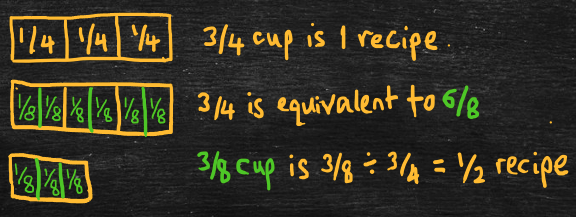
Here’s another example,

• Arithmetic problem: Solve 2/3 ÷ 4/9.
• Word problem: Lina has read 2/3 of the textbook, while Mari has read 4/9 of the textbook. Proportionally, how much more of the textbook has Lina read than Mari?
• Solve by expressing fractions using common denominators and dividing the numerators.
• 2/3 ÷ 4/9 = 6/9 ÷ 4/9 = 6 ÷ 4 = 3/2, so Lina has read 3/2 or 1  1/2 (one and a half) times more of the textbook than Mari.

How many units in one group?

A/B ÷ C/D represents, “How many units are in one group if A/B units are divided into C/D groups?” To scale C/D groups to one group, multiply by D/C, so also scale A/B units by multiplying by D/C. For example,

• Arithmetic problem: Solve 3/8 ÷ 3/4.
• Word problem: Saima uses 3/8 of a cup of sugar to make 3/4 of a recipe. How much sugar is in a whole recipe?
• Solve using “invert and multiply.”
• 3/8 ÷ 3/4 = 3/8 x 4/3 = 1/2, so one recipe has 1/2 a cup of sugar.
• Again, a recipe is a “group” and the cups of sugar are the units, but now we’re finding the fraction of a cup of sugar in one recipe: 3/8 of a cup of sugar ÷ 3/4 of a recipe = 1/2 of a cup of sugar per recipe.
• Equivalently, 1/2 of a cup of sugar per recipe times 3/4 of a recipe equals 3/8 of a cup of sugar.

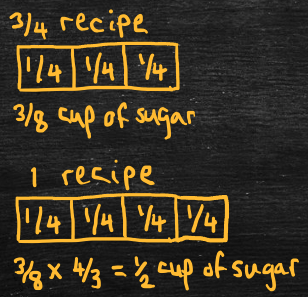
Here’s another example:

• Arithmetic problem: Solve 2/3 ÷ 4/9.
• Word problem: Skylar fills 4/9 of a jar with 2/3 of a pound of jelly beans. How many pounds of jelly beans does Skylar need to fill the whole jar?
• Solve using “invert and multiply.”
• 2/3 ÷ 4/9 = 2/3 x 9/4 = 3/2, so Skylar needs 3/2 or 1  1/2 (one and a half) pounds of jelly beans to fill the whole jar.

The video below works through some examples of word problems for dividing fractions.