3.1: Multiplying integers

Partial-products method

To multiply two integers together, multiply each combination of digits in the two integers, taking account of place value. Then, add these “partial-products” together. For example,

• 46 x 27
• = (40 + 6) x (20 + 7)    [expand integers into tens and ones]
• = (7 + 20) x (6 + 40)    [re-order to match usual layout in diagram below]
• = (7 x 6) + (7 x 40) + (20 x 6) + (20 x 40)    [use the distributive property, i.e., FOIL: First, Outer, Inner, Last]
• = (7 ones x 6 ones) + (7 ones x 4 tens) + (2 tens x 6 ones) + (2 tens x 4 tens)
• = 42 + 280 + 120 + 800
• = 1242

Common method

The common method uses the same idea of partial-products, but writes the calculations more compactly. For example,

• 46 x 27
• = (46) x (20 + 7)    [expand second integer into tens and ones]
• = (7 + 20) x (46)    [re-order to match usual layout in diagram below]
• = (7 x 46) + (20 x 46)    [use the distributive property]
• = 322 + 920
• = 1242

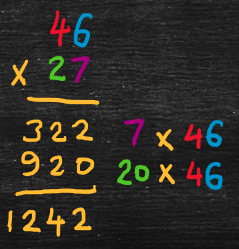
The video below works through some examples of multiplying integers.